The Conditional
The Conditional truth table has the most potential to be counterintuitive. Also, the conditional relation is arguably the most fundamental one of all the logical connectives. In fact, in most axiomatic systems, the first axioms are stated as conditionals. So, it is critical that we have understanding of what the conditional relation really is, as it could well be argued that all of logic hangs on it!
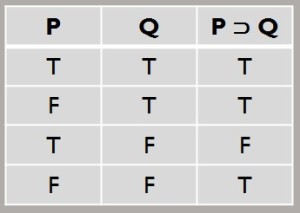
For convenience, here is the truth table again, so we can refer to it on this page.
First, let us start by saying that we are using the “material conditional.” There are other sorts of conditionals, such as counterfactual and subjunctive conditionals. It is far, far beyond the scope of this seminar to address those.
The material conditional is the “simple” one, and it is in fact the “strictly logical” one. Finally, in the same way that we can express exclusive disjunction using inclusive disjunction, the other forms of conditional rest upon the material conditional. So, it is sufficient for our purposes in our context, and it is indeed the foundation of all of our thinking in conditional terms.
When we say “P implies Q,” or we say, “Well, the implication of what you are saying is…,” we are using the material conditional. And in the vast majority of cases where we are trying to express “if, then,” we are using the material conditional.
So, let’s go through the rows of the truth table one by one and get a sense of what they are doing.
Imagine, as before, that P contains “there is fire,” and Q contains “there is heat.” So, in conditional form, the relation is simply: “If there is fire, then there is heat.”
In the first row of the truth table we see a scenario in which there is both fire and heat. So, “there is fire” is true, and “there is heat” is true. Obviously and intuitively, our complex proposition, “If there is fire, then there is heat” is true in that scenario.
Let us skip the second row for a moment and come back to it. The second row is the one that can feel most counterintuitive to people, so I will explain it in detail.
In the third row, we see a scenario in which there is fire, but there is no heat. Well, that is exactly the sort of scenario in which we would say that we have a “falsifying instance” showing that the complex proposition is false. When I say, “If there is fire, then there is heat,” what I am trying to express is exactly that “whenever there is fire, there is heat,” and this very scenario shows that it is not the case that whenever there is fire, there is heat. So, this truth table row expresses the one sort of scenario that would demonstrate a conditional claim to be false.
In the fourth row, we have a scenario in which there is neither fire nor heat. I have claimed, “Whenever there is fire, there is heat,” and this scenario does nothing to demonstrate that claim to be false.
And important point emerges at this juncture. Why shouldn’t we presume a claim is false unless it is proved to be true? Why does the truth table presume a true conditional, even when both parts of the conditional are false?
There is more to say than really can be said in this particular course. I will mention charity (always charity), which presumes the best about arguments and even particular claims, until they are shown to not be worthy of “the best”. I will mention how these connectives are derived from axioms and the internal consistency of classical logic with this row of the truth table being what it is. I could mention other things, and I know that I am only “hand waving” here to merely mention the foregoing points. But I will instead focus on the answer that is most relevant to this very course.
All propositions emerge in the context of sentences that “assert as true”. Whenever I make a claim, I am asserting that what I am saying is the case. So, all propositions “come with” at least the assertion, if not the presumption, of truth. This row of the truth table acknowledges that fact by saying, “Fine, it’s true unless shown otherwise.”
And this presumption correlates with how we will approach scientific theory evaluation! Theories are asserted as true. And we then look for falsifications of the theory, presuming all along that at least the author of the theory asserts it as true.
The third row of the truth table shows the scenario that can falsify a conditional claim, and the fourth row shows a scenario in which we simply have no “evidence” about whether the claimed conditional relation holds or not! So, it is treated as true; it was asserted as true, and nothing indicates otherwise.
That Counterintuitive Second Row!
Well, if the fourth row needed some explanation, the second row needs far more explanation!
Here is a scenario in which there is no fire, yet there is heat. But I claimed that “whenever there is fire, there is heat.” Many people have the sense that in the absence of fire, we literally know nothing about fire’s relation to heat. Such people would be inclined to say something like, “Well, you claimed that fire somehow produces heat. But that’s an empty claim in every case where there is no fire. I could just as well be saying something like, ‘If the moon is made of green cheese, then I have hands.’ The first part has nothing whatsoever to do with the second part, and that second row of the truth table is capturing exactly my ‘green-cheese moon that produces hands’ scenario. Ridiculous!”
And, sure enough, it seems patently false to claim, “If the moon is made of green cheese, then I have hands”!
Here is the problem with all such intuitions….
Every one of these sorts of intuitions rests upon putting content into the ‘P’s and ‘Q’s and then saying, “Ridiculous”!
The difficulty in educating people’s intuitions on this sort of thing is that most people are locked into the realm of content. But logic is entirely formal, devoid of content! And the reason people get caught in formal fallacies is because they get tricked by the content into thinking illogically.
Nixon’s Intentional Formal Fallacy
A classic example of how content can confuse reasoning is illustrated by how Richard Nixon attempted (quite successfully for quite some time) to trick the American people into believing he had “no prior knowledge” of the Watergate break-in.
John Dean had testified to Senate of the existence of Nixon’s secret taping system, and Dean claimed that some of the tapes included conversational evidence of Nixon’s complicity in and prior knowledge of the Watergate break-in. Obviously, if such tapes existed, and the Senate could get their hands on the tapes, Nixon’s presidency would be quite immediately over. So, in some early public appearances on the subject, Nixon attempted to sway public opinion his way, and he did so by arguing (paraphrased) this way:
“If such secret tapes existed, then I would be a crook. But there are no such tapes as the Senate is demanding. I am NOT a crook!”
Most Americans were swayed by this “reasoning,” as they were swayed by the pathos with which Nixon delivered the content of his argument. Thus, they did not recognize the formal fallacy expressed by the argument.
Let’s change up the content and see if you catch it:
“If it is raining, then the streets are wet. It is not raining, Therefore the streets are not wet.”
Ah, now you see that there are countless ways that the streets can be wet without rain! Street sweepers, broken fire hydrants… the list goes on and on. Just because it is not raining does not mean that the streets are not wet!
Yet, this is such a common formal fallacy, that it even has a name: Denying the antecedent. And the form of Nixon’s argument is exactly that formal fallacy:
P ⊃ Q
~P
——————-
~Q
Look at Nixon’s content: P contains “secret tapes exist showing that I was complicit in Watergate,” and Q contains “I am a crook.” Now, review Nixon’s argument, and you see that he was employing (many, including me, believe: intentionally) the formal, logical fallacy of denying the antecedent.
This is bad reasoning regardless of the content! You might catch it with certain content and yet be tricked with other content. As long as you are thinking of how “plausible” the content sounds, you can be tricked! The power of logic in argument analysis is that it abstracts away from the content, strips away all the confusion, and shows the formal relations for what they really are!
Back to That Pesky Second Row
The same content problem is going on with most people’s intuitions regarding that second row of the truth table. With certain content in the ‘P’s and ‘Q’s, they find the row to be counterintuitive. Yet, with entirely other content in the ‘P’s and ‘Q’s, they have little or no trouble with it.
If the conditional statement is “Whenever there is fire, there is heat,” most people don’t get hung up on the second row at all! They recognize that the statement is true, even in scenarios in which there is no fire. In fact, in both the second and fourth rows, the scenarios in which there is no fire, people intuitively recognize that the absence of fire has no bearing on the fact that the claimed relation is a true one.
And that is what matters: the relation! The truth table is expressing a logical relation between two propositions. It is expressing absolutely nothing about content! It is capturing only how truth-functionality works for the logical relation, and nothing more.
When we are talking about fire and heat, you almost certainly agree that the truth table is expressing that relation correctly. It is only when we start talking about things like moons made of green cheese that people balk at rows two and four, particularly two, of the truth table. And it is for that exact reason that I use examples like moons made of green cheese! I want you to learn how easy it is to have your reasoning powers corrupted and confused by cleverly-cast content.
In both scenarios in which the antecedent is false, the conditional statement is truth-functionally true!
Some Critical Terms
I have repeatedly used the term “antecedent” now, and in context it has been clear. But now it is time to formally define two terms that will be used constantly: antecedent and consequent.
The antecedent is “the thing that goes before,” and you will see it represented formally as the sentence letter that precedes the conditional symbol.
The consequent is “the thing that follows,” and you will see it represented formally as the sentence letter that follows the conditional symbol. It helps to think of the consequent as “the consequence of the first thing being true,” or, “the consequence of the antecedent.”
Just think in terms of “before” and “after,” remember that a “consequence” always comes “after,” and you’ll have it.
These two terms closely relate to two other terms: sufficient condition and necessary condition.
The antecedent is always the sufficient condition, just as fire is a sufficient condition for producing heat.
The consequent is always the necessary condition, just as it is necessary for fire that there be heat.
A sufficient condition is a condition that is “enough by itself” to produce the consequent.
A necessary condition is “something that must be present” for the antecedent to be the case.
If fire indeed does produce heat, then heat is indeed necessary for there to be fire. Notice that “necessary” does not mean “enough”! Heat does not always get you fire! But fire does always get you heat. So, fire is sufficient for heat, and heat is necessary for fire.
Again, the antecedent is always the sufficient condition, and the consequent is always the necessary condition.
Why Conditionals Matter
Of all the logical connectives, the conditional is the only one that can capture causality. Whatever causality “really” is, it is certainly a sufficient and necessary condition relation. Indeed, Kant actually defined causality in terms of the conditional, and this is one of many things I believe Kant nailed!
Science continually uses conditionals in its own causal inferences. So, we are treating science charitably to consider its notion of causality in conditional terms.
The relation between theory and evidence can best be cast as a conditional, and that relation is absolutely central to our whole course!
Finally, certain inferences, such as modus ponens and modus tollens, are central to both the practice and the philosophy of science; and these inferential forms are dependent on the conditional.
So, for this course, there is no more important logical relation than the conditional!
Now, I have mentioned a few inferential forms, and it is time to express those formally. We will reference them many times.
Modus Ponens (valid)
P ⊃ Q
P
—————–
Q
If it is raining, then the streets are wet.
It is raining.
Therefore, the streets are wet.
Modus Tollens (valid)
P ⊃ Q
~Q
—————–
~P
If it is raining, then the streets are wet.
The streets are not wet.
Therefore, it is not raining.
Denying the Antecedent (invalid, formal fallacy)
P ⊃ Q
~P
—————–
~Q
If it is raining, then the streets are wet.
It is not raining.
Therefore, the streets are not wet.
Affirming the Consequent (invalid, formal fallacy)
P ⊃ Q
Q
—————–
P
If it is raining, then the streets are wet.
The streets are wet.
Therefore, it is raining.
Summary
The material conditional is fundamental to logic and to how we think in propositional terms. It can be counterintuitive as long as you are thinking about content and not in a strictly truth-functional way. But the more you contemplate what the truth table is actually expressing, the more your intuitions acknowledge that the relation could not work in any other way.
The conditional is also central to the subject of this course, as everything from causality to the relations science itself expresses are best captured by the conditional.
The conditional is also the basis of some of the most common inferences we employ every day, as well as the basis of some of the most common mistakes we make in reasoning when we get tricked by plausible-sounding content.
Going forward, we will be very systematic in our reliance upon the conditional in our analysis of science’s arguments regarding evolutionary theory.